[NOIP2002 普及组] 过河卒

题目描述

棋盘上 $A$ 点有一个过河卒，需要走到目标 $B$ 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，$A$ 点 $(0, 0)$、$B$ 点 $(n, m)$，同样马的位置坐标是需要给出的。

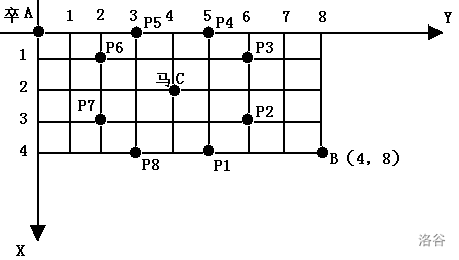
现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 $B$ 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

样例 #1

样例输入 #1

6 6 3 3

样例输出 #1

6

提示

对于 $100 \%$ 的数据，$1 \le n, m \le 20$，$0 \le$ 马的坐标 $\le 20$。

【题目来源】

NOIP 2002 普及组第四题

先简化问题
假如不考虑马，卒从(0,0)到(x,y)的方法有多少种？
根据排列组合知识，可知有

$$ C_{x+y}^{x}种可能 $$

那么假设(x1,y1)有障碍
结果将变为

$$ C_{x+y}^{x}-C_{x1+y1}^{x1}-C_{(x+y)-(x1+y1)}^{x-x1}种可能 $$

因此，只要计算出马所占有的不能走的位置即可